A Basic Case Study Addressing Multi-Scale Modelling of Drug Delivery Using COMSOL

By Grigoriy Kimaev and Luis A. Ricardez-Sandoval
Department of Chemical Engineering, University of Waterloo

Product Cost: Free-of-charge to all CACHE member departments. $50 to all non-members.

Contact cache@cache.org if you are interested in obtaining this case study.

Coordinated by the CACHE Design Task Force, a basic case study for product design has been prepared for distribution by CACHE. The case study has been class tested on many occasions as part of a computational laboratory for a third-year design course on micro and nano systems offered to Nanotechnology Engineering undergraduate students at the University of Waterloo and reviewed/critiqued by task-force members.

The present case study involves the implementation, simulation and design of nanoparticle drug-delivery systems. This case study is designed to equip students with the translatable and widely applicable skill of creating multi-scale multi-physics models in COMSOL where the data is shared among the scales via coupled variables. Key questions address the size and number (concentration) of nanoparticles, and initial drug concentrations, for prescribed rates of drug delivery. The mass-transfer problem involves a coupled PDE and ODE to be solved using COMSOL multi-physics. Both written and video instructions are provided to assist instructors and students in formulating the COMSOL simulation and interpreting the results.

In this study, multiscale modelling is conceived as a way to describe systems that evolve at different spatial and time scales. Coupling events that take place at different scales in certain applications are key to accurately predict process performance, product quality, and productivity. In addition, these multiscale models are suitable tools that can be embedded within optimization formulations to conduct studies involving optimal product design, process operation and online control. Multiscale models like that considered in this work emerge in such real-life applications as semiconductor manufacturing (e.g. thin-film deposition (Chaffart & Ricardez-Sandoval, 2018, Rasoulian & Ricardez-Sandoval, 2014, 2016)), the design of energy storage devices (e.g. Lithium-ion batteries (Ramadesigan et. al., 2012)), chemical product manufacturing (e.g. catalytic flow reactors (Chaffart & Ricardez-Sandoval, 2017)), pharmaceutical product design (e.g. drug delivery (Nayhouse et. al., 2015)), and others.

Consider first, a brief introduction to the drug-release kinetics model:

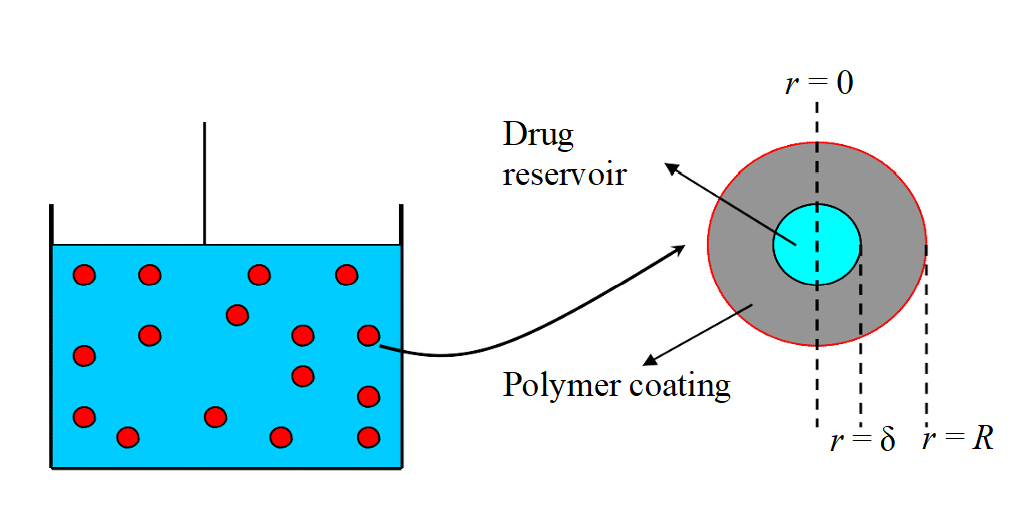
The drug, say for pharmaceutical applications such as cancer therapy, is placed in a drug reservoir, assumed to be a solid sphere of radius δ, which is encapsulated by a polymer substance; e.g., a nano-gel. This last layer is used to control the drug delivery rate. The entire nano-particle is assumed to be a solid sphere of a given radius, R. A storage tank filled with N_p nano-particles is used to study the drug concentration profiles in a given system; e.g., a human body. The tank is assumed to be well stirred and the density of the fluid is assumed to be constant. The temperature in the tank is also assumed to be constant. This problem can be considered as a multi-scale problem since the microscopic diffusion taking place in the nano-particle is coupled with a macroscopic mass balance inside the tank.

For an introduction to teaching mass-transfer from nano-particles in transport-phenomena courses, as well as the multi-scale PDE-ODE model, the reader is referred to Ortiz-Rodriguez et al. (2010) for more details.

The CACHE Design Task Force envisions this CACHE product being used in two ways:

Transport Phenomena and Advanced ChE Modelling Courses

It is a practical mass-transfer problem to convey nanoliter quantities of drugs from nano-particles into blood streams. The mass-transfer by Fick’s Law diffusion from a nano-particle in spherical geometry is fairly straight-forward, but coupling it to mass-transfer into a well-mixed blood stream requires a finite-element solution, well beyond the skills of most undergraduate students. COMSOL Multiphysics makes this possible; however, most undergraduate ChE students need instruction on how to couple these models since this specific subject is not often covered in transport phenomena courses offered in most of the ChE undergraduate programs in North America. Note: students would still need some preliminary experience using COMSOL Multiphysics, as provided, for example, by Wilkes (2017).

Using these teaching materials (written and video), ChE undergraduate students will learn how a basic multiscale model can be implemented in COMSOL Multiphysics and consider different product designs of the nanoparticle that contains the drug. For instance, select different radii, nano-gel polymers, initial drug concentrations, numbers (concentrations) of particles. Also, ChE undergraduate students can assess how product design decisions will impact the system’s dynamics; e.g., the time variations of drug concentrations, both in the nano-particles and in the blood streams. Such case studies can add a practical dimension to transport-phenomena courses.

Product Design Course

One can view nano-particle drug release as a basic functional product-design, multiscale problem. In this case, the designer has various needs in mind. Then, the question becomes one of designing a profitable product to satisfy those needs. Stated differently, the drug-delivery system needs to be designed with the goal of delivering a specific amount of drug over a particular timeframe (e.g., a day, a week, or a month), with constraints imposed on the minimum and maximum daily dose. Specifying the radii of the drug reservoir and the polymer coating, as well as the initial drug concentration in the reservoir, and the number of nanoparticles in the storage tank, would allow engineers and scientists to fulfill the design specifications.

The following open-ended conceptual design problem can be considered:

One key component that drives drug therapy is the rate at which drugs are administered to patients. Depending on the application, slow or fast drug delivery rates can be controlled by setting optimal product design specifications. It is often found that product performance is limited by the model specifications considered when performing optimal product design. For instance, model parameters are typically assumed to be perfectly known a priori whereas in reality some of these parameters are subject to uncertainty (Kimaev & Ricardez-Sandoval, 2017, 2018). Taking parameter uncertainty into account would therefore result in optimal product designs that are less sensitive to uncertainty. Assume that the diffusivity coefficient in the drug reservoir layer (D_r) has been estimated using experimental data. A preliminary statistical analysis shows that D_r can be approximated using a Gaussian distribution with mean 2.5x10^-16 m²/s and standard deviation 7.49x10^-17 m²/s. Assume that the rest of the model parameters remain constant (see Table 1 in the documentation). Given these assumptions and the multiscale drug delivery model presented in this case study, find the initial drug concentration in the reservoir and thickness of the polymer coating that would be required to achieve a final (steady-state) drug concentration in the tank above 1x10^-8 mol/m³. Your proposed product design specification should take into account the variability in the diffusivity coefficient. Compare the optimal product design under uncertainty to the design obtained under the assumption that D_r is set to its mean (expected) value. Solve these problems under three instances; i.e., on each instance set the number of particles (N_p) to 2x10¹⁰, 1x10¹⁰ and 4x10¹⁰, respectively. Note that adding the number of particles as an additional product design decision variable may further improve product design at the expense of solving challenging (mixed-integer) optimization formulations. In addition, the following questions could be considered:

• What initial drug concentration in the reservoir (the C_A0 value) is necessary to cause the steady-state drug concentration in the tank to be 1x10^-7 mol/m³ when 4x10¹⁰ is the maximum number of nanoparticles? In reality, would it be feasible to achieve this C_A0 value for a drug reservoir with a 10 nm radius?
• Suppose that 30 nm is the minimum polymer coating thickness that can prevent the coating from rupturing and prematurely releasing the contents of a drug reservoir with the 10 nm radius. If C_A0 is 20 mol/m³ and the diffusivity coefficient of the polymer coating is as specified in Table 1 in the documentation, is it possible to achieve the steady state concentration in the tank in under 3 hours?

This is an open-ended product-design project, well-suited for a group of 3-4 senior ChE undergraduate students. Note that a similar time-delivery, functional product-design problem for herbicide particles (to eliminate weeds) is posed and solved as Example 5.2 in Seider et al. (2017). Please note that the open-ended problem does not necessarily have a unique solution; hence, the authors did not create a tutorial guide for this problem.

Product Composition

This product is comprised of:

• Problem statement/definition (in a PDF file – 15 pages) for students in transport phenomena and simulation courses – giving specifics of preparing COMSOL simulation models for the coupled PDE-ODE models.
• Multimedia step-by-step instructions, provided in a .EML file, to be followed by students in creating COMSOL models and carrying out simulations.
• POWER POINT slides summarizing the drug delivery model and specifications for presentation by instructors.

References

Chaffart, D., & Ricardez-Sandoval, L. A. (2017). Robust dynamic optimization in heterogeneous multiscale catalytic flow reactors using polynomial chaos expansion. Journal of Process Control, 60, 128–140.

Chaffart, D., & Ricardez-Sandoval, L. A. (2018). Optimization and Control of a Thin Film Growth Process: A Hybrid First Principles/Artificial Neural Network Based Multiscale Modelling Approach. Computers and Chemical Engineering, 119, 465–479.

Kimaev, G., & Ricardez-Sandoval, L. A. (2017). A comparison of efficient uncertainty quantification techniques for stochastic multiscale systems. AIChE Journal, 63(8), 3361–3373.

Kimaev, G., & Ricardez-Sandoval, L. A. (2018). Multilevel Monte Carlo applied to chemical engineering systems subject to uncertainty. AIChE Journal, 64(5), 1651–1661.

Nayhouse, M., Tran, A., Kwon, J. S.-I., Crose, M., Orkoulas, G., & Christofides, P. D. (2015). Modeling and control of ibuprofen crystal growth and size distribution. Chemical Engineering Science, 134, 414–422.

Ortiz-Rodriguez, E., Vasquez-Arenas, J. & Ricardez-Sandoval, L. A. (2010). An Undergraduate Course in Modeling and Simulation of Multiphysics Systems. Chemical Engineering Education, 44(4), 299-305.

Ramadesigan, V., Northrop, P. W. C., De, S., Santhanagopalan, S., Braatz, R. D., & Subramanian, V. R. (2012). Modeling and Simulation of Lithium-Ion Batteries from a Systems Engineering Perspective. Journal of the Electrochemical Society, 159(3), R31–R45.

Rasoulian, S., & Ricardez-Sandoval, L. A. (2014). Uncertainty analysis and robust optimization of multiscale process systems with application to epitaxial thin film growth. Chemical Engineering Science, 116, 590–600.

Rasoulian, S., & Ricardez-Sandoval, L. A. (2016). Stochastic nonlinear model predictive control applied to a thin film deposition process under uncertainty. Chemical Engineering Science, 140, 90–103.

Seider, W.D., Lewin, D.R., Seader, J.D., Widagdo, S., Gani, R., & Ng, K.-M., Product and Process Design Principles, 4^th Ed., Wiley, 2017.

Wilkes, J. O., Fluid Mechanics for Chemical Engineers, 3^rd Ed., Prentice-Hall, 2017.